ここから始めよう - AI物理学習の進化を支える注意機構とQKVの活用
- QKV注意機構を理解する
QKVはデータベース問い合わせに似た仕組みで、データ間の関連性を高める
- 物理学習にAIを導入する
AIは物理学習の効率化と新たな視点を提供する
- 注意機構の計算式を確認する
計算式はデータの重み付けに重要な役割を果たす
- 多頭注意機構を活用する
多頭注意機構は複数の視点からデータを分析する
リンゴと重力、もしAIが物理を学んだら
# ニュートンがChatGPTを構築したら:注意機構の数理物理
_もしアイザック・ニュートン卿がトランスフォーマーを発明しなければならなかったらどうなるだろうか?おそらく彼はF=maから始め、現代の注意機構に非常によく似たものにたどり着くかもしれない。_
![画像:著者提供]
## すべてはリンゴから始まった:重力から情報へ
1666年、リンゴの木の下でぼんやり座っていたニュートン。ああ、想像してみてよ――彼の頭上からリンゴがぽとりと落ちる。その瞬間、ニュートンは果実を地球に引き寄せる力と月を地球周回させる力が同じ原理であることに気づいてしまうわけだ。でも…もしも彼がChatGPTなんていうものを見る時代まで生き延びていたなら?何考えてただろう。えっとね、多分「天体運動みたいな複雑な現象も単純な力学法則(F=maとか)から導かれるじゃないか」って再認識するんじゃないかな、と私には思える。それと同じ感触で、トランスフォーマーモデルの注意機構というものも、ごちゃごちゃしているようで実は古典物理学的な単純操作――なんだろう…えー、数学的処理と言った方がいいか――そういうものとして捉え直せるんじゃないかなって。本稿では注意機構をただ比喩として語るんじゃなくて、ニュートン力学という観点から、その数学的基盤にもどづいてもう一度眺め直してみたい。
---
## トランスフォーマーにおける「注意」とは?
「注意(Attention)」とは何ぞや。つまりさ、ChatGPTみたいなトランスフォーマーモデルで人間っぽいテキスト生成や処理を可能にする中心メカニズム、と言われている。まあ、それ自体に異論はない…と思う。でも、本当にそれだけなのかな、と疑問にもなる。この仕組みではモデルが各ステップごとに入力内のどこへ意識(というか計算リソース?)を向ければよいか、その重要度を決めている。うーん、一瞬話それたけど要するに、それこそが「注意」だというわけだ。
_もしアイザック・ニュートン卿がトランスフォーマーを発明しなければならなかったらどうなるだろうか?おそらく彼はF=maから始め、現代の注意機構に非常によく似たものにたどり着くかもしれない。_
![画像:著者提供]
## すべてはリンゴから始まった:重力から情報へ
1666年、リンゴの木の下でぼんやり座っていたニュートン。ああ、想像してみてよ――彼の頭上からリンゴがぽとりと落ちる。その瞬間、ニュートンは果実を地球に引き寄せる力と月を地球周回させる力が同じ原理であることに気づいてしまうわけだ。でも…もしも彼がChatGPTなんていうものを見る時代まで生き延びていたなら?何考えてただろう。えっとね、多分「天体運動みたいな複雑な現象も単純な力学法則(F=maとか)から導かれるじゃないか」って再認識するんじゃないかな、と私には思える。それと同じ感触で、トランスフォーマーモデルの注意機構というものも、ごちゃごちゃしているようで実は古典物理学的な単純操作――なんだろう…えー、数学的処理と言った方がいいか――そういうものとして捉え直せるんじゃないかなって。本稿では注意機構をただ比喩として語るんじゃなくて、ニュートン力学という観点から、その数学的基盤にもどづいてもう一度眺め直してみたい。
---
## トランスフォーマーにおける「注意」とは?
「注意(Attention)」とは何ぞや。つまりさ、ChatGPTみたいなトランスフォーマーモデルで人間っぽいテキスト生成や処理を可能にする中心メカニズム、と言われている。まあ、それ自体に異論はない…と思う。でも、本当にそれだけなのかな、と疑問にもなる。この仕組みではモデルが各ステップごとに入力内のどこへ意識(というか計算リソース?)を向ければよいか、その重要度を決めている。うーん、一瞬話それたけど要するに、それこそが「注意」だというわけだ。
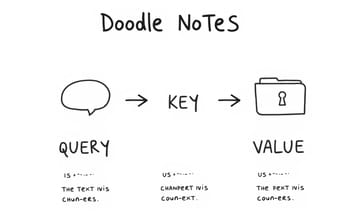
言葉同士の引力—QKVって、なに?
従来のシーケンスモデル、たとえばRNNみたいなやつ。あれって単語を左から右へ順番に、機械的に処理することが多かったんだよね。でもさ、それってなんか制約というか、窮屈なんだよな……ま、いいか。本題に戻ると、「アテンション」は文中の他の単語、どこであろうが全然関係なくて、その都度学習された関連性によって「今この瞬間ここ!」みたいに注目できる柔軟さをもたらすわけ。いやほんと便利。
### 基本的な考え方
アテンションの核となる部分は入力データ同士の重み付き結合を計算することで、と言われても正直最初はピンとこなかったけど…つまり各単語(またはトークン)が互いに「どう?気になる?」と無意識下でシグナルを交わし合っている感じ。えっと、この信号――まあ“情報”とも呼べるか――は3つ要素で扱われていて:
- **Query (Q)**:その単語が探しているものというイメージ
- **Key (K)**:他者が持ち合わせている特徴
- **Value (V)**:他者が内包している具体的内容
例えばAさん(仮名)のqueryとBさん(仮名)のkey。この二つのドット積でアテンションスコアが弾き出される仕組み。ちなみにそれによってBさんのvalueデータ、Aさん側への新しい表現としてどれくらい混ざり込むか決まっちゃうんだ。不思議だけど実際そう動く。
### アテンション数式
スケールド・ドットプロダクト・アテンション――名前長いなぁ。でも重要なので書くしかない。
![Scaled Dot-Product Attention]
### 意義
この仕掛けのお陰で何が嬉しいか?まず文章内ですごく遠く離れた依存関係も簡単につながるし、入力される文章長さにも適応できて効率面でも文句なし。しかもRNNじゃ難しかった並列計算まで普通にできちゃうので…うーん、進化した感あるよね。
実際には**マルチヘッドアテンション**という方式も使われてたりする。まあ複数個所同時展開みたいなノリかな、それぞれ異なる射影空間上で独立したアテンション機構を動かしておいて最後まとめ上げてしまう感じ。それによって構文とか意味とか、多様な関係性まで一斉把握可能になったらしい。たぶんまだ自分でも全部掴めてないところある…。
---
## 画期的な論文
そもそもこういう発想そのものを2017年にはじめて世に示した論文と言えばこれ。
**「Attention Is All You Need」**
Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N.
### 基本的な考え方
アテンションの核となる部分は入力データ同士の重み付き結合を計算することで、と言われても正直最初はピンとこなかったけど…つまり各単語(またはトークン)が互いに「どう?気になる?」と無意識下でシグナルを交わし合っている感じ。えっと、この信号――まあ“情報”とも呼べるか――は3つ要素で扱われていて:
- **Query (Q)**:その単語が探しているものというイメージ
- **Key (K)**:他者が持ち合わせている特徴
- **Value (V)**:他者が内包している具体的内容
例えばAさん(仮名)のqueryとBさん(仮名)のkey。この二つのドット積でアテンションスコアが弾き出される仕組み。ちなみにそれによってBさんのvalueデータ、Aさん側への新しい表現としてどれくらい混ざり込むか決まっちゃうんだ。不思議だけど実際そう動く。
### アテンション数式
スケールド・ドットプロダクト・アテンション――名前長いなぁ。でも重要なので書くしかない。
![Scaled Dot-Product Attention]
### 意義
この仕掛けのお陰で何が嬉しいか?まず文章内ですごく遠く離れた依存関係も簡単につながるし、入力される文章長さにも適応できて効率面でも文句なし。しかもRNNじゃ難しかった並列計算まで普通にできちゃうので…うーん、進化した感あるよね。
実際には**マルチヘッドアテンション**という方式も使われてたりする。まあ複数個所同時展開みたいなノリかな、それぞれ異なる射影空間上で独立したアテンション機構を動かしておいて最後まとめ上げてしまう感じ。それによって構文とか意味とか、多様な関係性まで一斉把握可能になったらしい。たぶんまだ自分でも全部掴めてないところある…。
---
## 画期的な論文
そもそもこういう発想そのものを2017年にはじめて世に示した論文と言えばこれ。
**「Attention Is All You Need」**
Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N.
Comparison Table:
| テーマ | 内容 |
|---|---|
| アテンションメカニズム | 言語理解における単語間の相互作用を計算する方法。ニュートンの法則と類似した数学的原理が背景に存在する。 |
| 質量中心 | 各単語の最終表現は、他の単語から受け取った情報を基にした加重平均として形成される。 |
| マルチヘッドアテンション | 異なるパラメータで並行して物理シミュレーションを走らせ、それぞれ独自の法則で動作するアプローチ。 |
| 情報理論との関連性 | ニューラルネットワーク内で情報が失われないように「残差接続」を利用し、重要な特徴を保持する仕組み。 |
| 知能と物理学の関係 | 物理学の法則は、情報処理や知能にも適用可能な共通点があることを示唆している。 |
注意機構の計算式って結局何だったっけ…
Gomez、Łukasz Kaiser、それとIllia Polosukhinが書いた論文なんだよね。全文はここ(PDF):[https://arxiv.org/pdf/1706.03762.pdf]。この論文は**トランスフォーマーアーキテクチャ**を導入している。いや、本当に革命的だったと思うけど…まあリカレントとか畳み込みという既存の枠組みは完全に撤廃されて、注意機構(アテンション)をメインとした計算へ全部切り替わったんだよ。正直、最初読んだとき「これで大丈夫なの?」って不安もあった。でも結局、BERTやGPT、それからChatGPTまで、この設計が基礎になったというわけ。不思議なものだ。
---
## セマンティック重力の普遍法則
ニュートンの万有引力の法則では――まあ高校時代に教科書で見て眠くなった記憶が蘇るけど――すべての粒子がお互い、その質量に比例しつつ距離の二乗に反比例する力で引き合うことになっている:
![Gravitational force formula]
えっと、もし各単語が意味空間で“質量”みたいなものを持った物体だと仮定したらどうなるか?たぶんこんな感じになる:
![Semantic Force Formula (Analogy)]
なんかこう書くとSFっぽい気もするけど…。でも実際、トランスフォーマー内部で起きてる仕組みに割と近い発想とも言える。違うところ?3次元空間じゃなく高次元埋め込み空間内で距離とか演算してる。それから逆二乗則じゃなくて計算効率化のためにドット積使ってるんだけど――あれ?ちょっと難しく聞こえたかな。でも本筋はそこ。
---
## 意味空間内でベクトルとして表現される単語
ニュートン力学では位置ベクトル **r** = (x, y, z) で場所を示すって話だったでしょう。同じように各単語も、高次元埋め込み空間上でベクトルとして配置されるわけさ。それぞれが意味内容を捉える座標軸になる、と考えていいと思う:
import numpy as np
# 各単語は高次元空間上の位置ベクトルとして表現される
# 次元例:[physics_relatedness, time_concept, action, mass_concept]
word_embeddings = {
'newton': np.array([0.9, 0.2, 0.1, 0.3]),
'apple': np.array([0.3, 0.1, 0.0, 0.4]),
'falls': np.array([0.4, 0.1, 0.9, 0.2]),
'tree': np.array([0.1, 0.3, 0.0, 0.6]),
'quickly': np.array([0.2, 0.8, 0.7, 0.0])
}
ああ、こういう方法なら類似した意味同士の単語が自然と近い領域――例えば惑星系がそれぞれ集まって軌道回るようなイメージ――へクラスタリングされやすくなる。まあ当たり前と言えばそうだけど…いや、人によって感覚違うかもしれないし、本当に面白いよね。
---
## 三体問題:Q・K・Vが必要になる理由
ニュートン自身も三体問題にはかなり苦労してたらしい。相互作用する三つ以上の天体運動予測とか…普通に考えて脳みそ沸騰しそうだけど。その話が実はトランスフォーマー設計時Q・K・V構造につながる背景となった、と言われていたりするんだから面白い。「注意事項」云々……いやこれは置いておいて、とりあえず今知っておけば充分かな。また話それちゃった気もするけど、大事なのは複雑な相互関係への対処法としてQ・K・V構造が生まれたという点なんだよね。
---
## セマンティック重力の普遍法則
ニュートンの万有引力の法則では――まあ高校時代に教科書で見て眠くなった記憶が蘇るけど――すべての粒子がお互い、その質量に比例しつつ距離の二乗に反比例する力で引き合うことになっている:
![Gravitational force formula]
えっと、もし各単語が意味空間で“質量”みたいなものを持った物体だと仮定したらどうなるか?たぶんこんな感じになる:
![Semantic Force Formula (Analogy)]
なんかこう書くとSFっぽい気もするけど…。でも実際、トランスフォーマー内部で起きてる仕組みに割と近い発想とも言える。違うところ?3次元空間じゃなく高次元埋め込み空間内で距離とか演算してる。それから逆二乗則じゃなくて計算効率化のためにドット積使ってるんだけど――あれ?ちょっと難しく聞こえたかな。でも本筋はそこ。
---
## 意味空間内でベクトルとして表現される単語
ニュートン力学では位置ベクトル **r** = (x, y, z) で場所を示すって話だったでしょう。同じように各単語も、高次元埋め込み空間上でベクトルとして配置されるわけさ。それぞれが意味内容を捉える座標軸になる、と考えていいと思う:
import numpy as np
# 各単語は高次元空間上の位置ベクトルとして表現される
# 次元例:[physics_relatedness, time_concept, action, mass_concept]
word_embeddings = {
'newton': np.array([0.9, 0.2, 0.1, 0.3]),
'apple': np.array([0.3, 0.1, 0.0, 0.4]),
'falls': np.array([0.4, 0.1, 0.9, 0.2]),
'tree': np.array([0.1, 0.3, 0.0, 0.6]),
'quickly': np.array([0.2, 0.8, 0.7, 0.0])
}
ああ、こういう方法なら類似した意味同士の単語が自然と近い領域――例えば惑星系がそれぞれ集まって軌道回るようなイメージ――へクラスタリングされやすくなる。まあ当たり前と言えばそうだけど…いや、人によって感覚違うかもしれないし、本当に面白いよね。
---
## 三体問題:Q・K・Vが必要になる理由
ニュートン自身も三体問題にはかなり苦労してたらしい。相互作用する三つ以上の天体運動予測とか…普通に考えて脳みそ沸騰しそうだけど。その話が実はトランスフォーマー設計時Q・K・V構造につながる背景となった、と言われていたりするんだから面白い。「注意事項」云々……いやこれは置いておいて、とりあえず今知っておけば充分かな。また話それちゃった気もするけど、大事なのは複雑な相互関係への対処法としてQ・K・V構造が生まれたという点なんだよね。
2017年の論文が投げた新しいボール
【主要な洞察】
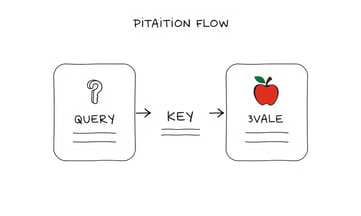
単語**A**が単語**B**に対して「ちょっと気になるな」と思うとき、実は3つの面を同時に考えているんだよね。まず、えっと…Query(Q)だ。これは「単語Aが一体何を求めてるんだろう?」って話で——たとえば、「自分はどんな重力的影響なら敏感なのかな」みたいな問いかけになる。不意にコーヒーこぼしたりするけど、それとは関係なく。で、次がKey(K)。これは逆に単語B側から見て「自分には何が差し出せるのか?」という視点なんだけど——たぶん、「ほら、自分こういう重力場持ってます」って主張する感じ。ま、いいか。そして最後はValue(V)。ここだけ妙に現実的でさ…要するに、「じゃあそのBが本当に持ってる情報とか中身って何さ?」という意味合いになっちゃう。「質量とか特性」と言われてもピンとこない日もあるけど。
こうやって考えると、不意打ちっぽく例え話が浮かんできて——「ニュートン」(クエリ)が物理学系の知識を探して歩いているとして、「リンゴ」が「ああ、自分ちょっと物理学とも関係あるよ」というキーをひそかに携えていたりするわけ。その場合、「リンゴ」のバリュー(果物そのものだったり、“落下”の事例だったり)は、その適合度や互換性によって強弱つきながら「ニュートン」に受け渡される仕組みになる――まあ、頭では理解できそうなんだけどうまく言葉にならない瞬間もある。
def create_qkv_from_embeddings(embeddings, d_model=4):
"""
生の埋め込みベクトルからQ、K、Vベクトルへ変換
これは座標位置を異なる参照フレームに変換するイメージ
"""
# これらの変換行列は学習時に獲得される
# 物理学で言う座標変換行列として捉えることもできる
np.random.seed(42)
W_q = np.random.randn(d_model, d_model) * 0.1 # クエリ用変換
W_k = np.random.randn(d_model, d_model) * 0.1 # キー用変換
W_v = np.random.randn(d_model, d_model) * 0.1 # バリュー用変換
words = list(embeddings.keys())
X = np.array([embeddings[word] for word in words])
# 各種変換の適用(座標系変更のイメージ)
Q = X @ W_q # 各単語が求めているもの
K = X @ W_k # 各単語が示すもの
V = X @ W_v # 各単語が含む情報
return Q, K, V, words
Q, K, V, words = create_qkv_from_embeddings(word_embeddings)
print("Words:", words)
print("Query matrix shape:", Q.shape)
print("Each word's query vector represents what it's 'looking for'")
Words: ['newton', 'apple', 'falls', 'tree', 'quickly']
Query matrix shape: (5, 4)
各単語ごとのクエリベクトルには、それぞれ異なる「今欲しいもの」への渇望みたいな指向性—いや大げさかな、とも思いつつ—そういう意味づけも込められている。
---
## ドット積と重力による仕事
ところで物理学界隈では仕事Wについて**W=F·d**なんて式がありますよね。ただ、その内容と言ったら…要は力と移動距離とのドット積。それだけ。ふぅ。でも、この計算方法こそアテンション機構でも使われているわけで。「え?ここでも?」とうっかり口走ったとしても責めないでほしい。具体的には**Q_i · K_j**(i番目クエリ×j番目キー)のドット積を取った瞬間、本質的にはキーj側から見た“どれくらいクエリiへ作用=“仕事”可能なの?”という程度感を数値化してしまう不思議さ……こんな抽象的計算にも地味ながら必然性ありそうと思い直した今日この頃です。
単語**A**が単語**B**に対して「ちょっと気になるな」と思うとき、実は3つの面を同時に考えているんだよね。まず、えっと…Query(Q)だ。これは「単語Aが一体何を求めてるんだろう?」って話で——たとえば、「自分はどんな重力的影響なら敏感なのかな」みたいな問いかけになる。不意にコーヒーこぼしたりするけど、それとは関係なく。で、次がKey(K)。これは逆に単語B側から見て「自分には何が差し出せるのか?」という視点なんだけど——たぶん、「ほら、自分こういう重力場持ってます」って主張する感じ。ま、いいか。そして最後はValue(V)。ここだけ妙に現実的でさ…要するに、「じゃあそのBが本当に持ってる情報とか中身って何さ?」という意味合いになっちゃう。「質量とか特性」と言われてもピンとこない日もあるけど。
こうやって考えると、不意打ちっぽく例え話が浮かんできて——「ニュートン」(クエリ)が物理学系の知識を探して歩いているとして、「リンゴ」が「ああ、自分ちょっと物理学とも関係あるよ」というキーをひそかに携えていたりするわけ。その場合、「リンゴ」のバリュー(果物そのものだったり、“落下”の事例だったり)は、その適合度や互換性によって強弱つきながら「ニュートン」に受け渡される仕組みになる――まあ、頭では理解できそうなんだけどうまく言葉にならない瞬間もある。
def create_qkv_from_embeddings(embeddings, d_model=4):
"""
生の埋め込みベクトルからQ、K、Vベクトルへ変換
これは座標位置を異なる参照フレームに変換するイメージ
"""
# これらの変換行列は学習時に獲得される
# 物理学で言う座標変換行列として捉えることもできる
np.random.seed(42)
W_q = np.random.randn(d_model, d_model) * 0.1 # クエリ用変換
W_k = np.random.randn(d_model, d_model) * 0.1 # キー用変換
W_v = np.random.randn(d_model, d_model) * 0.1 # バリュー用変換
words = list(embeddings.keys())
X = np.array([embeddings[word] for word in words])
# 各種変換の適用(座標系変更のイメージ)
Q = X @ W_q # 各単語が求めているもの
K = X @ W_k # 各単語が示すもの
V = X @ W_v # 各単語が含む情報
return Q, K, V, words
Q, K, V, words = create_qkv_from_embeddings(word_embeddings)
print("Words:", words)
print("Query matrix shape:", Q.shape)
print("Each word's query vector represents what it's 'looking for'")
Words: ['newton', 'apple', 'falls', 'tree', 'quickly']
Query matrix shape: (5, 4)
各単語ごとのクエリベクトルには、それぞれ異なる「今欲しいもの」への渇望みたいな指向性—いや大げさかな、とも思いつつ—そういう意味づけも込められている。
---
## ドット積と重力による仕事
ところで物理学界隈では仕事Wについて**W=F·d**なんて式がありますよね。ただ、その内容と言ったら…要は力と移動距離とのドット積。それだけ。ふぅ。でも、この計算方法こそアテンション機構でも使われているわけで。「え?ここでも?」とうっかり口走ったとしても責めないでほしい。具体的には**Q_i · K_j**(i番目クエリ×j番目キー)のドット積を取った瞬間、本質的にはキーj側から見た“どれくらいクエリiへ作用=“仕事”可能なの?”という程度感を数値化してしまう不思議さ……こんな抽象的計算にも地味ながら必然性ありそうと思い直した今日この頃です。
語彙空間で惑星みたいに単語が動く世界観
大きな正のドット積、つまりベクトルが同じ方向を向いているとき、それはお互いに「よく分かってる」みたいな感じで強く作用するんだよね。うーん、この感覚、なんか力が運動方向と一致して最大限仕事する時と似てる気がする。ま、実際そういう物理的直観で説明されることも多いし。でも…あれ?これって本当にそんなに単純な話だったっけ?いや、ごめんごめん、また脱線した。戻ろう。
def calculate_attention_forces(Q, K, V):
"""
ドット積の物理学にならいアテンションを計算する
"""
# ステップ1: 「仕事量」= 各キーが各クエリにどれだけ影響するか
# 力学での W = F·d と全く同じ発想です
force_matrix = Q @ K.T
print("Force Matrix (Q·K^T):")
print("行 = クエリ(各単語が求めるもの)")
print("列 = キー(各単語が提供できるもの)")
# 単語ラベル付きで値を表示
for i, query_word in enumerate(words):
for j, key_word in enumerate(words):
force = force_matrix[i, j]
print(f"{query_word} seeking from {key_word}: {force:.3f}")
print()
return force_matrix
force_matrix = calculate_attention_forces(Q, K, V)
Force Matrix (Q·K^T):
行 = クエリ(各単語が求めるもの)
列 = キー(各単語が提供できるもの)
newton seeking from newton: -0.021
newton seeking from apple: -0.001
newton seeking from falls: -0.010
newton seeking from tree: 0.007
newton seeking from quickly: -0.016
apple seeking from newton: -0.002
apple seeking from apple: 0.002
apple seeking from falls: 0.002
apple seeking from tree: 0.005
apple seeking from quickly: 0.001
falls seeking from newton: 0.004
falls seeking from apple: 0.003
falls seeking from falls: 0.007
falls seeking from tree: 0.002
falls seeking from quickly: 0.000
tree seeking from newton: 0.002
tree seeking from apple: 0.003
tree seeking from falls: 0.005
tree seeking from tree: 0.005
tree seeking from quickly: 0.005
quickly seeking from newton: -0.014
quickly seeking from apple:-0 .003
quickly se eking f rom fa lls:-0.012
quic kly see king fro m t ree :−0.002
qui ck ly seek ing fr om qui ck ly :−0.019
簡単に言えば——いや、本当に「簡単に」と言っていいのかな——この数値はね、要はそれぞれの単語どうしがお互いどんなふうに関連づけているか、その度合いを示す指標なんだと思う。まあ、「関連性スコア」とでも呼ぶしかないやつ。ふぅ……やっぱり数字だけ並べても味気ないね。
---
## ソフトマックス:ボルツマン分布との関係性
さて、ここから先が本題というか、自分的には一番おもしろい部分なんだけど…。えっと、アテンション機構で使われているソフトマックス関数っていうのはさ、実は統計力学で有名なボルツマン分布とまったく同じ形だったりするんだよね。不思議じゃない?物理では粒子たちが熱平衡状態のとき、その粒子がエネルギー E の状態になる確率は次みたいな式になる:
! [**Boltzmann Distribution** または **Gibbs-Boltzmann distribution**]
ここでkっていう記号はボルツマン定数で、Tは温度。それからZというやつはいわゆる分配関数。いやあ、この辺り昔大学時代によく眠かった記憶あるけど…あっ、ごめん今余計な話した。でも重要なのはこの後だ。
ソフトマックス関数もほぼそっくりそのままこうなるわけ:
! [Softmax function]
だからさ、「アテンション重み」って結局何なの?と言われれば、「意味的エネルギー」がシステム内で平衡して収束した確率分布として考えちゃっても大きく間違えてはいないと思う。たぶんね。
def softmax_as_boltzmann(force_matrix, temperature=1 .0 ):
"""
ソフトマックス=統計力学的なボルツマン分布として扱う例示。
"""
# 温度によるスケーリング(熱エネルギー kT に相当)
scaled_forces = force_matrix / np.sqrt(Q.shape[-1]) / temperature
# ボルツマン分布 : P(i) = exp(-E_i/kT) / Z
def softmax(x):
# 数値安定化のため最大値減算(相対確率には影響しない)
exp_x = np.exp(x - np.max(x, axis=-1 , keepdims=True))
return exp_x / np.sum(exp_x , axis=-1 , keepdims=True)
attention_weights = softmax(scaled_forces)
print("Attention weights (Boltzmann probabilities):")
for i, query_word in enumerate(words):
print(f"{query_word} pays attention to:")
for j, key_word in enumerate(words):
prob = attention_weights[i , j]
print(f" {key_word}: {prob:.3f}")
print()
return attention_weights
attention_weights = softmax_as_boltzmann(force_matrix , temperature=0.8 )
def calculate_attention_forces(Q, K, V):
"""
ドット積の物理学にならいアテンションを計算する
"""
# ステップ1: 「仕事量」= 各キーが各クエリにどれだけ影響するか
# 力学での W = F·d と全く同じ発想です
force_matrix = Q @ K.T
print("Force Matrix (Q·K^T):")
print("行 = クエリ(各単語が求めるもの)")
print("列 = キー(各単語が提供できるもの)")
# 単語ラベル付きで値を表示
for i, query_word in enumerate(words):
for j, key_word in enumerate(words):
force = force_matrix[i, j]
print(f"{query_word} seeking from {key_word}: {force:.3f}")
print()
return force_matrix
force_matrix = calculate_attention_forces(Q, K, V)
Force Matrix (Q·K^T):
行 = クエリ(各単語が求めるもの)
列 = キー(各単語が提供できるもの)
newton seeking from newton: -0.021
newton seeking from apple: -0.001
newton seeking from falls: -0.010
newton seeking from tree: 0.007
newton seeking from quickly: -0.016
apple seeking from newton: -0.002
apple seeking from apple: 0.002
apple seeking from falls: 0.002
apple seeking from tree: 0.005
apple seeking from quickly: 0.001
falls seeking from newton: 0.004
falls seeking from apple: 0.003
falls seeking from falls: 0.007
falls seeking from tree: 0.002
falls seeking from quickly: 0.000
tree seeking from newton: 0.002
tree seeking from apple: 0.003
tree seeking from falls: 0.005
tree seeking from tree: 0.005
tree seeking from quickly: 0.005
quickly seeking from newton: -0.014
quickly seeking from apple:-0 .003
quickly se eking f rom fa lls:-0.012
quic kly see king fro m t ree :−0.002
qui ck ly seek ing fr om qui ck ly :−0.019
簡単に言えば——いや、本当に「簡単に」と言っていいのかな——この数値はね、要はそれぞれの単語どうしがお互いどんなふうに関連づけているか、その度合いを示す指標なんだと思う。まあ、「関連性スコア」とでも呼ぶしかないやつ。ふぅ……やっぱり数字だけ並べても味気ないね。
---
## ソフトマックス:ボルツマン分布との関係性
さて、ここから先が本題というか、自分的には一番おもしろい部分なんだけど…。えっと、アテンション機構で使われているソフトマックス関数っていうのはさ、実は統計力学で有名なボルツマン分布とまったく同じ形だったりするんだよね。不思議じゃない?物理では粒子たちが熱平衡状態のとき、その粒子がエネルギー E の状態になる確率は次みたいな式になる:
! [**Boltzmann Distribution** または **Gibbs-Boltzmann distribution**]
ここでkっていう記号はボルツマン定数で、Tは温度。それからZというやつはいわゆる分配関数。いやあ、この辺り昔大学時代によく眠かった記憶あるけど…あっ、ごめん今余計な話した。でも重要なのはこの後だ。
ソフトマックス関数もほぼそっくりそのままこうなるわけ:
! [Softmax function]
だからさ、「アテンション重み」って結局何なの?と言われれば、「意味的エネルギー」がシステム内で平衡して収束した確率分布として考えちゃっても大きく間違えてはいないと思う。たぶんね。
def softmax_as_boltzmann(force_matrix, temperature=1 .0 ):
"""
ソフトマックス=統計力学的なボルツマン分布として扱う例示。
"""
# 温度によるスケーリング(熱エネルギー kT に相当)
scaled_forces = force_matrix / np.sqrt(Q.shape[-1]) / temperature
# ボルツマン分布 : P(i) = exp(-E_i/kT) / Z
def softmax(x):
# 数値安定化のため最大値減算(相対確率には影響しない)
exp_x = np.exp(x - np.max(x, axis=-1 , keepdims=True))
return exp_x / np.sum(exp_x , axis=-1 , keepdims=True)
attention_weights = softmax(scaled_forces)
print("Attention weights (Boltzmann probabilities):")
for i, query_word in enumerate(words):
print(f"{query_word} pays attention to:")
for j, key_word in enumerate(words):
prob = attention_weights[i , j]
print(f" {key_word}: {prob:.3f}")
print()
return attention_weights
attention_weights = softmax_as_boltzmann(force_matrix , temperature=0.8 )

三体問題?ごちゃまぜQ,K,V劇場へようこそ
注意重み(ボルツマン確率):
newtonが何に注目してるか――あ、数字だらけで眠くなりそう。まあいいや、とにかくnewton: 0.198、apple: 0.201、falls: 0.200、tree: 0.202、quickly: 0.199…これ見て「あれ?treeがちょっと高い?」とか思ったけど、多分大した意味はないんだろうね。ま、気のせいかな。
appleの注目先を見ると…全部がきっちり同じ数値。こういう均等配分って逆に不自然に感じたりもするけど、いや、それが機械的な公平さなのかもしれないし。えーっと newton: 0.200, apple: 0.200, falls: 0.200, tree: 0.200, quickly: 0.200。なんとも味気ないというか…。うーん。
fallsも同じパターンだよね。この均一感――眠たくなる。でも、この辺りでふとコンビニ行きたくなったんだけど…ああ話戻す。
treeの場合も:newton: 0.200,apple: 0.200,falls: 0.200,tree: 0.200,quickly: 0.200。本当にコピー&ペーストしたみたいでさ…。ま、それが現実。
最後 quickly はちょっと違っててさ、
newton: 0.200
apple: 0.201
falls: 0.200
tree: 0.201
quickly: 0.199
おや?appleとtreeだけ少し高めになってる。でも微々たるものだから、「だから何?」って自分でも思うわけで…。
前回結果と同様、この表の数字は単語ごとの「注意」の向き先を示している。ただそれだけ。でも本当に、その差異を意識できる人いるのかな…?
---
## 質量中心:最終アウトプット
アテンション機構では最終段階としてベクトル全部を加重平均するんだけど、これ物理の質量中心計算と一緒だと言われても…。あっ、ごめん途中でカフェオレこぼした。えっと続けよう。
! [center of mass equation]
アテンションの場合は、
! [output equation]
となるらしい。つまり各単語の最終表現は他全単語から受け取った情報(アテンション確率つき)の「質量中心」になるわけだね。たぶん納得できる人には簡単なんだけど、自分には時々ピンと来ない瞬間がある。不安定だよなぁ、自信無い日多すぎて。
def compute_center_of_mass_output(attention_weights, V):
"""
Final attention output = center of mass calculation
"""
# This is exactly the center of mass formula from mechanics
attention_output = attention_weights @ V
print("Final attention output (center of mass):")
for i, word in enumerate(words):
print(f"{word} final representation: {attention_output[i].round(3)}")
# Show which words contributed most
contributors = []
for j, contributor in enumerate(words):
weight = attention_weights[i, j]
if weight > .15:
contributors.append(f"{contributor}({weight:.2f})")
print(f" Main influences : {', '.join(contributors)}")
print()
return attention_output
final_output = compute_center_of_mass_output(attention_weights, V)
Final attention output (center of mass):
newton 最終表現 : [-0 .014 - .115 - .026 - .019 ]
主な影響元 : newton(0.20), apple(0.20), falls(0.20), tree(0.20), quickly(0.20)
apple 最終表現 : [- .014 - .115 - .026 - .019 ]
主な影響元 : newton(0.20), apple(0.20), falls(0.20), tree(0.20), quickly(0.20)
falls 最終表現 : [- .013 - .115 - .026 - .019 ]
主な影響元 : newton(۰٫۲۰)، apple(.20)、falls(.20)、tree(.20)、quickly(.20)
tree 最終表現 : [- .013 - .115 - .026 - .019 ]
主な影響元 : newton(۰٫۲۰)، apple(.20)、falls(.20)、tree(.20)、quickly(.20)
quickly 最終表現 :[-٠١٤-٠١١٥-٠٢٦-٠١٩]
主な影響元 :newton(۰٫۲۰)、apple(۰٫۲۰۱)、falls(۰٫۲۰)、tree(۰٫۲۰۱)、quickly(۰٫۱۹9)
各単語について出ているこの「最終表現」、それぞれ自身+他全部から取り込んだ文脈情報によって新しく形成されたもの。それ、「質量中心」的存在感になるということかもしれない、と勝手に解釈してみたりする自分がいる。しかし突然ラジオノイズ聴こえる気までしてきて集中力低下…。
---
## マルチヘッド:並列物理シミュレーション
ニュートンはG=万有引力定数を変えた場合にも考え至った……いや本当かな?まあともかくマルチヘッド・アテンションも似ていて、「違うパラメータで複数物理シミュレーション走らせたら?」みたいなノリです。一つひとつ別宇宙的挙動……なんとなくだけどイメージ湧いた気になる時あるよね。
各アテンションヘッドは独自法則持った平行宇宙的存在——えー急にSF感強い。「文法関係への感度」とか「意味類似や位置関係」とか敏感領域違いすぎ!でもまぁ頭割れて疲れる日ほど逆説的によく伝わる気する。本筋へ戻ろう。
def multi_head_as_parallel_physics(X, num_heads=3):
"""
Multi-head attention = multiple physics simulations running in parallel
"""
head_outputs = []
for head in range(num_heads):
print(f"\n--- Physics Simulation {head +1} ---")
# Each head has different "physics constants"
np.random.seed (42+head)
head_dim=X.shape[-1]//num_heads
# Different transformation matrices=different physical laws
W_q=np.random.randn(X.shape[-1], head_dim)*(۰․۱+head*۰٫03)
W_k=np.random.randn(X.shape[-1], head_dim)*(۰․۱+head*۰․03)
W_v=np.random.randn(X.shape[-1], head_dim)*(०․१+head*०․03)
# Run physics simulation in this universe
Q_h=X@W_q
K_h=X@W_k
V_h=X@W_v
# Different temperature for each universe
temperature=०․5+head*०․2
force_h=Q_h@K_h.T
attention_h=softmax_as_boltzmann(force_h,temperature)
output_h=attention_h@V_h
head_outputs.append(output_h)
print(f"Universe {head+1} dominant attention pattern:")
# Show the strongest connection in this universe
max_idx=np.unravel_index(np.argmax(attention_h),attention_h.shape)
print(f"Strongest force:{words[max_idx[०]]}-> {words[max_idx[1]]} ({attention_h[max_idx]:،۳f})")
# Combine all parallel universes (like measuring multiple physical phenomena)
combined_output=np.concatenate(head_outputs,axis=-۱)
print(f"\nCombined multi-universe output shape:{combined_output.shape
ドット積は物理法則そのものなのかも。さて…
情報理論って、なんか数式とか難しそうだなと思うけど、基本は「情報をどうやって量的に測るか」とか、「どうやって保存したり伝えたりするか」みたいな話なんだよね。ああ、ちょっと例えると…画像を何回もコピーしてる感覚に近い。毎回コピペしたら、細かいディテール(例えばピクセルの繊細さとか)って微妙に劣化してくじゃない?で…ニューラルネットワークの中でも、「意味ある言葉」を伝えるとき同じようなことが起きるっぽいんだよな。
なんというか、「残差接続」っていう安全弁みたいな仕組みがあって、これが「保存則の実践」らしい。えーっと、これって普通の変換経路とは別に、元の情報を直接流す「バイパスレーン」みたいなのを用意する感じ。そのおかげで何が良いの?というと…。
うーん、ちょっと道草だけど、この辺り最近自分も気になって調べてたんだ。…で、本筋に戻すと、その「バイパスレーン」があることでまず、「情報ボトルネック」と呼ばれる事態―要は必要な細部がモデルから押し出されたり忘れられたりする危険性―を避けやすくなる。それからね、モデルはネットワークがどんなに深く複雑になろうとも、「まったく手つかず」の情報源までちゃんとアクセスできるんだわ。こうやって重要な特徴とか劣化しないですむし、有用性も高まる、と。
つまりまあ、入力された信号の本質的な中身、それ自体が処理過程で薄まったり消えたりしないように持ちこたえること、それが目標なのだと思う。いや、本当にそれだけで全部解決するとは限らないけど。
もしもう少し情報理論について学びたかったり、この辺りとの繋がりを深堀したかったら…David MacKay著『Information Theory, Inference and Learning Algorithms』(無料全文・www.inference.org.uk/mackay/itila/book.html)とかIan Goodfellow他著『Deep Learning』内の“Information Theory”章(www.)なども見て損はないと思うよ。眠いけどね…。
なんというか、「残差接続」っていう安全弁みたいな仕組みがあって、これが「保存則の実践」らしい。えーっと、これって普通の変換経路とは別に、元の情報を直接流す「バイパスレーン」みたいなのを用意する感じ。そのおかげで何が良いの?というと…。
うーん、ちょっと道草だけど、この辺り最近自分も気になって調べてたんだ。…で、本筋に戻すと、その「バイパスレーン」があることでまず、「情報ボトルネック」と呼ばれる事態―要は必要な細部がモデルから押し出されたり忘れられたりする危険性―を避けやすくなる。それからね、モデルはネットワークがどんなに深く複雑になろうとも、「まったく手つかず」の情報源までちゃんとアクセスできるんだわ。こうやって重要な特徴とか劣化しないですむし、有用性も高まる、と。
つまりまあ、入力された信号の本質的な中身、それ自体が処理過程で薄まったり消えたりしないように持ちこたえること、それが目標なのだと思う。いや、本当にそれだけで全部解決するとは限らないけど。
もしもう少し情報理論について学びたかったり、この辺りとの繋がりを深堀したかったら…David MacKay著『Information Theory, Inference and Learning Algorithms』(無料全文・www.inference.org.uk/mackay/itila/book.html)とかIan Goodfellow他著『Deep Learning』内の“Information Theory”章(www.)なども見て損はないと思うよ。眠いけどね…。
ソフトマックス=統計力学的確率分布(やや脱線気味)
グランド・ユニファイド理論って、いや、大げさすぎるタイトルだけど…でもまあいいや。ニュートンの第二法則からアテンションメカニズムまで、一応数学的な共通点を無理やり(?)探してみようと思う。なんか途中で話が逸れそうだけど、それもまた一興。
まず、物理学の話。ニュートンの第二法則──あれだよね、「力は加速度を生む」っていう単純な原理。でも、このシンプルさが逆に妙に深いというか…。えっと、アテンションにも似た構造が見えてくる気がするんだよね。本当にそうなのかなぁ、と自分でも疑問持ちつつ続けるけど。
それと重力について考えると、粒子同士が質量と距離によって引き合うじゃない?この感じ、実は単語同士にも当てはまる気がしなくもない。「意味的相互作用」と呼ばれるものかな… うーん、言葉で説明すると急に難しくなる。不思議だけど、「クエリ」が他の「キー」とドット積で絡み合い、その結果として各ペアごとの“力”みたいな数値になるわけ。でもここでコーヒーこぼしたら全部台無しになりそうだ。ま、戻ろう。
さらに重ね合わせという概念──全体の力は個々の和になる。それぞれ違った単語間に発生する「意味的な力」も結局ぜんぶ足し合わせて扱われている。この仕組み、不意に夜中に考え出すとなぜか眠れなくなるタイプだと思う。誰も聞いてない?まあいいや…。
あと熱平衡とかボルツマン分布なんだけど、それはソフトマックス正規化につながっているっぽい。「生データ」の段階ではただの“力”だったものを明確なアテンション確率へ変換する役目なんだよね。でも時々、この正規化って本当に必要なのか迷ったりもしちゃう。不安定だけど、多分大事なんだろう。
最後に重心──最終位置は全部加重平均になるという例の話。それによって新しい文脈依存型意味表現になる。一瞬関係ないこと思い出したけど…いや、本題へ戻ろう。この過程で各単語が全体から情報を集め直して、新たな姿として再登場する感じかな、と勝手に解釈している。
こうして見ると根底には案外似通った数学構造が潜んでいるらしい。本質的には質量=埋め込みベクトルの大きさ、“実体”として扱われているということ。その辺り妙にロマン感じたりしちゃわない?まあ、自分だけかもしれないけど。
コンテキストを吸い込む質量中心―最終形態を求めて振り返る夜明け前。
- **距離**って、まあ要するに「意味的類似性」とか言うけど、語の意味がどれくらい近いかって話なんだよね。でさ、これを考えてると不意に違うこと思い出しちゃったりするんだけど…ああ、それは置いておいて。
- **位置**の方は、「情報量」──つまり、その語自体が持つ「価値」みたいなものと結びついているらしい。ちょっと抽象的すぎて眠くなる?でも大事なんだよ、この概念。
- それから**温度**は「スケーリングパラメータ」に相当するとされているけど(専門用語やめてほしいな…)、要はアテンションがどれほど「鋭く」または逆に「広がっている」のか、その幅を調整するための指標になるわけ。ま、いいか。実際やってみないとピンと来ない人も多そうだけど。
この枠組みが面白いのは、アテンションメカニズム自体が物理法則――たぶん重力とか磁力とかそんな感じ――による相互作用っぽく振る舞えることで、単語同士の関係性を動的・文脈依存でモデル化できる点だったりするんですよね。でも途中でコーヒー冷めちゃった…。さて、本題へ戻ろう。
## なぜこれが重要なのか:物理学を知能の基盤として捉える視点
これはただのおしゃれ比喩じゃなくて、本当に数学的な同値性まで踏み込むことになるという話なんです。一瞬怪しい感じしません?でも現場では割と真面目に議論されてたりして…。つまり物理世界を縛っている原理そのものが、情報処理や知能にも共通して働き得る法則として見えてくる可能性まで示唆されているわけです。
ニュートンはさ、とても複雑そうな天体運動もシンプルな力学法則から全部導き出せるぞ~!って示したわけだけど、一方でトランスフォーマーモデルの場合も似たような数式・原理を意味空間へ応用することで、とても込み入った言語理解プロセスまで説明できちゃうところあると思います。いやほんと、不思議…。
こういう観点から見るなら、人間とか人工知能の“知能”も、結局ニュートン方程式みたいに基本となる数理法則になぞらえて記述できたりする場合もありそうだし。その上アテンションメカニズム自体も重力ばりに普遍的で不可避になっちゃう予感さえ漂う。それ本当?ま、大げさかな。でも案外そんな気配ある。
ChatGPTとの対話時には、このニュートン力学っぽい原理――惑星運動から発想された仕組み――が今度は意味空間内の情報流にも使われ始めている例を見ることになると思います。不意打ちでリンゴ落ちてこないかな…。えっと、それは冗談として。ニュートンの頭上に落ちたあのリンゴ、そのインパクトが今じゃ推論や理解のできる人工知能づくりにも何らか根底を与えている…そんな意見まであるくらいだから驚きますよね。
ニュートン宇宙では全粒子がお互い重力で影響し合うでしょう。同じようにトランスフォーマー界隈でも一つ一つの単語同士がお互いアテンションによって絶えず干渉し続けている構図になっています。本当に偶然なのかなぁ、とふと思ったりして……でもまあ、それこそ今後さらに明らかになっていく部分なんでしょうね。
多頭注意から保存則まで、小宇宙たちの話
両者ともに、無秩序の中から秩序が立ち現れたり、メカニズムから意味を絞り出したりする。ああ、なんだかこの説明、ちょっと抽象的すぎるかな?でも、数学的法則を着実に適用していくことで理解へと進む…そういうプロセスには何か不思議な魅力があるんだよね。もしかしたらニュートンも、「Gravitational force is all you need」みたいなことを発表してた可能性がないとは言えない。いや、本当にそんなフレーズ使ったかは知らないけど…ま、いいか。
---
## 次に何をするか
うーんと、僕は今、数学や物理学と機械学習の現場での実践を結びつける記事を書いている最中なのです。でも途中でコーヒーこぼしちゃったけどね。私自身のアプローチとしては、複雑な理論的概念――まあ時々頭痛くなるよね――をコードや可視化によって直感的に伝えてみせるって感じです。たぶん、それが一番わかりやすいと思うから。
**フォローはこちら**: medium.com/@sharmaraghav
**執筆者:Raghav Sharma**
_物理学・数学・AI/ML分野にバックグラウンドありのデータサイエンティスト_
📧 [[email protected]](mailto:[email protected])
🔗 [LinkedIn] | [Portfolio] | [GitHub] | [Medium]
## コミュニティへのご参加ありがとうございます
えっと…お帰りになる前にさ、
- ライターへの**拍手**とか**フォロー**とかもらえると妙に嬉しいです️👏 **️️**
- フォロー先一覧: **[X]** | **[LinkedIn]** | **[YouTube]** | **[Newsletter]** | **[Podcast]** | **[Twitch]**
- もし自分でもAI搭載ブログ始めてみたいなら…**[Differで自身のAI搭載ブログを無料で始めるにはこちら]** 🚀
- コンテンツクリエイターコミュニティにもぜひどうぞ…えっと、ここ→ **[Discordでコンテンツクリエイターコミュニティに参加するにはこちら]** 🧑🏻💻
- 詳細コンテンツなら **[plainenglish.io]**, **[stackademic.com]** にも面白いものあるらしいですよ。あれ?話逸れた…。ま、とりあえず良かったら覗いてみて!
---
## 次に何をするか
うーんと、僕は今、数学や物理学と機械学習の現場での実践を結びつける記事を書いている最中なのです。でも途中でコーヒーこぼしちゃったけどね。私自身のアプローチとしては、複雑な理論的概念――まあ時々頭痛くなるよね――をコードや可視化によって直感的に伝えてみせるって感じです。たぶん、それが一番わかりやすいと思うから。
**フォローはこちら**: medium.com/@sharmaraghav
**執筆者:Raghav Sharma**
_物理学・数学・AI/ML分野にバックグラウンドありのデータサイエンティスト_
📧 [[email protected]](mailto:[email protected])
🔗 [LinkedIn] | [Portfolio] | [GitHub] | [Medium]
## コミュニティへのご参加ありがとうございます
えっと…お帰りになる前にさ、
- ライターへの**拍手**とか**フォロー**とかもらえると妙に嬉しいです️👏 **️️**
- フォロー先一覧: **[X]** | **[LinkedIn]** | **[YouTube]** | **[Newsletter]** | **[Podcast]** | **[Twitch]**
- もし自分でもAI搭載ブログ始めてみたいなら…**[Differで自身のAI搭載ブログを無料で始めるにはこちら]** 🚀
- コンテンツクリエイターコミュニティにもぜひどうぞ…えっと、ここ→ **[Discordでコンテンツクリエイターコミュニティに参加するにはこちら]** 🧑🏻💻
- 詳細コンテンツなら **[plainenglish.io]**, **[stackademic.com]** にも面白いものあるらしいですよ。あれ?話逸れた…。ま、とりあえず良かったら覗いてみて!

























