我們每天都在猜。今天會不會下雨?這支股票會漲還是會跌?... 老實說,我們生活裡到處都是這種不確定的事。
在充滿數據的世界裡,要怎麼跟這種「隨機性」相處,甚至把它變成可以信賴的預測?答案,嗯... 聽起來有點學術,但其實很直觀,就是「機率分佈」。
重點一句話
機率分佈,我自己是覺得,它就像一副數學眼鏡,幫我們在看似混亂的數據裡,看清楚那個「亂中有序」的模式。
為什麼這東西這麼重要?不只是算命而已
很多人聽到機率,可能就想到賭博或算命。但它在資料科學裡,是一個超級基礎又實用的工具。它不是告訴你「明天股票一定漲」,而是描繪出「各種可能結果的機率地圖」。
說到這個,我分享一個真實世界會發生的狀況。這比單純解釋理論有用多了。
想像一下,你是一個電商網站的分析師,你在看顧客每次購買商品的「數量」。你把幾千筆交易資料拉出來,畫了一張圖,想看看分佈狀況。

理論上,買 1-3 件商品的人應該最多,然後隨著數量增加,人數會平滑地變少。這很合理吧?但你卻在圖上看到一個很詭異的現象...
在「購買 5 件商品」的地方,數量突然不正常地往下掉,然後到 6 件又稍微回來一點。這就像牙齒掉了一顆,很不自然。
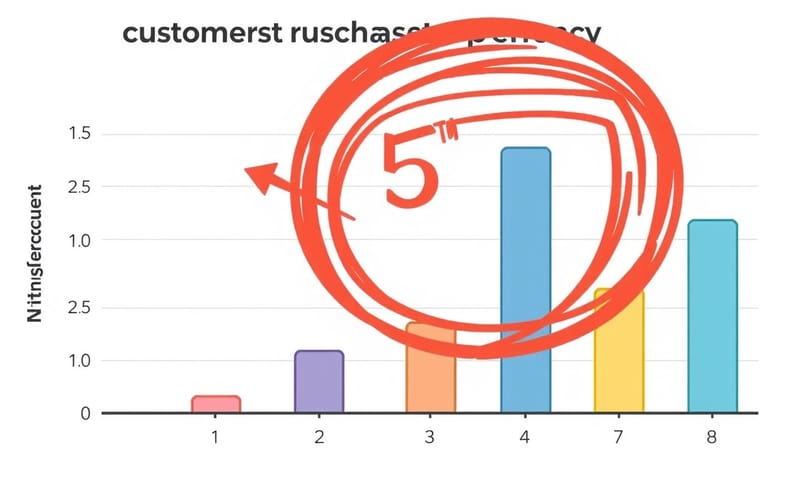
這個「凹痕」就是機率分佈給你的線索。它在說:「嘿,這裡有問題。」你可能就會回去追查,是不是當初紀錄資料的工程師手誤,把 `items=5` 的數據弄丟了?還是系統有 bug?
你看,這就不是算命。這是偵探工作。透過預期中的分佈形狀,去揪出現實數據裡的錯誤。這對庫存管理、商業決策都超重要的。
不只這樣,它也是很多機器學習演算法的基礎。還有啊,就像我們看中央氣象署說「降雨機率 80%」,這背後就是一套複雜的機率模型在跑,它也是基於過去大量的氣象數據,去建立一個關於「下雨」這件事的機率分佈。這點跟美國國家氣象局(NWS)的做法很像,都是用機率來溝通不確定性,只是背後的模型和地理參數不同。
那...資料有分種類,分佈當然也有
在談更深入的東西之前,要先知道我們處理的資料基本上分兩種,這會決定你用哪種分佈工具。
- 離散資料 (Discrete Data):就是那種一個一個,可以數的。像是你骰子丟出去,只會有 1, 2, 3, 4, 5, 6 這幾種結果。你不可能骰出 3.5。或者,一天收到的客訴信件數量、路口經過的車輛數,都是離散的。
- 連續資料 (Continuous Data):這種資料可以在一個範圍內,切到無限細。例如,人的身高、體重、花費的時間。一個人的身高可以是 175 公分,也可以是 175.1,甚至 175.12345... 公分,只要你的測量工具夠精準。
因為資料有這兩種型態,所以描述它們機率的「語言」也分成兩種。
兩種描述機率的「語言」:PMF vs. PDF
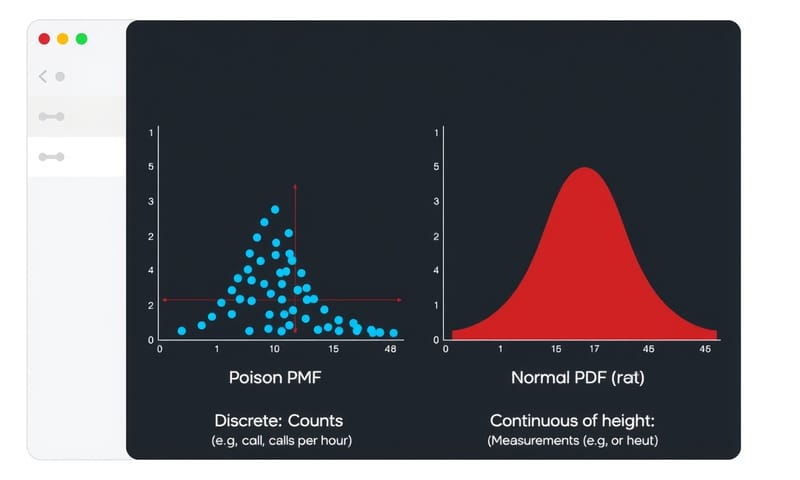
簡單講,PMF 是給離散資料用的,PDF 是給連續資料用的。它們都在做同一件事:描述每個數值出現的可能性有多大。
PMF,全名叫 Probability Mass Function(機率質量函數)。“Mass” 這個字很傳神,你可以想像,機率就像一坨一坨的質量,被「集中」在 1、2、3 這些特定的整數點上。所以你看它的圖,都是一根一根的柱子。
下面這段 Python 程式碼,就是用卜瓦松分佈(Poisson Distribution)來模擬一個離散事件,比如一個客服中心平均每小時接到 3 通電話,那實際接到 0, 1, 2... 通電話的機率各是多少。這在做人力排班或資源規劃時就蠻實用的。
import numpy as np
import matplotlib.pyplot as plt
from <a href="https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1284242" target="_blank" class="blogHightLight_css nobox">scipy</a>.stats import poisson
# 假設平均每小時接到 3 通電話
lambda_poisson = 3
# 我們想看 0 到 9 通電話的機率
x_discrete = np.arange(0, 10)
# 計算卜瓦松 PMF
pmf_poisson = poisson.pmf(x_discrete, mu=lambda_poisson)
# 算一下「接到電話 <= 2 通」的機率總和
highlight_x = np.arange(0, 3)
highlight_pmf = poisson.pmf(highlight_x, mu=lambda_poisson)
prob_poisson = np.sum(highlight_pmf)
# 畫圖
plt.style.use('seaborn-v0_8-darkgrid') # 讓圖好看一點
fig, ax = plt.subplots()
ax.stem(x_discrete, pmf_poisson, basefmt=" ", linefmt='b-', markerfmt='bo', label='P(X=k)')
ax.stem(highlight_x, highlight_pmf, basefmt=" ", linefmt='r-', markerfmt='ro', label='P(X ≤ 2)')
ax.set_title(f"卜瓦松 PMF (λ=3)\nP(X ≤ 2) 機率 = {prob_poisson:.3f}")
ax.set_xlabel("電話數量 (k)")
ax.set_ylabel("機率 P(X = k)")
ax.legend()
plt.show()
再來是 PDF,全名 Probability Density Function(機率密度函數)。“Density” 密度,就代表機率不是集中在某個點,而是「散佈」在一整個連續的區間上。所以你看它的圖,會是一條平滑的曲線,最有名的就是鐘形的常態分佈(Normal Distribution)。
對於連續資料,問「某個單一點」的機率是沒意義的,因為可能性有無限多個,所以任何一個點的機率都趨近於 0。我們通常問的是「某個範圍」的機率,例如身高在 170 到 180 公分之間的人有多少?這個機率,就是 PDF 曲線底下,從 170 到 180 那段的面積。
下面這段程式碼就是畫一個標準常態分佈(平均值 0,標準差 1),並且計算數值落在 -1 到 1 之間的機率。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 標準常態分佈參數
mu, sigma = 0, 1
x_continuous = np.linspace(-4, 4, 1000)
# 計算常態分佈 PDF
pdf_normal = norm.pdf(x_continuous, mu, sigma)
# 計算 P(-1 < X < 1) 的機率
mask = (x_continuous > -1) & (x_continuous < 1)
prob_normal = norm.cdf(1, mu, sigma) - norm.cdf(-1, mu, sigma)
# 畫圖
plt.style.use('seaborn-v0_8-darkgrid')
fig, ax = plt.subplots()
ax.plot(x_continuous, pdf_normal, 'b-', lw=2, label='PDF')
ax.fill_between(x_continuous[mask], pdf_normal[mask], alpha=0.3, color='red', label='P(-1 < X < 1)')
ax.set_title(f"常態分佈 PDF (μ=0, σ=1)\nP(-1 < X < 1) 機率 = {prob_normal:.3f}")
ax.set_xlabel("數值 (x)")
ax.set_ylabel("機率密度")
ax.legend()
plt.show()
常見錯誤與修正
老實說,剛接觸的時候,PMF 和 PDF 真的很容易搞混。我自己是覺得,用下面這個表來想會清楚很多。
| 比較項目 | PMF (給離散資料) | PDF (給連續資料) |
|---|---|---|
| 處理的資料類型 | 就是算「個」、「次」、「人」這種一個個的東西。像骰子點數、今天有幾個客訴... 不能是半個。 | 管的是可以無限切分的東西。身高、體重、時間... 175.1公分、175.11公分... 沒完沒了。 |
| 圖長怎樣 | 一根一根的柱子,像竹籤插在數字上。每根柱子的高度就是那個數字發生的機率。 | 一條平滑的曲線,像山丘或溜滑梯。我們看的不是「點」,是「區間」的面積。 |
| 機率怎麼看 | 很直接。直接看柱子多高就好。想知道 P(X=3)?就去看 3 那根柱子對應的 Y 軸數值。 | 看曲線底下的「面積」。單一一個點的機率... 基本上是零。所以都問「-1到1之間」的機率是多少。 |
| Y軸代表什麼 | 就...就是機率本人。所有柱子的高度加起來一定等於 1。 | 是「機率密度」,不是機率。它的大小可以超過 1,但整條曲線下的總面積一定等於 1。這點超多人搞錯。 |
所以,大致上是這樣。機率分佈不是什麼遙不可及的數學理論,它更像是一種強大的思維工具,幫助我們理解這個充滿不確定性的世界。從發現數據錯誤,到做出更合理的商業預測,都離不開它。
當然,今天只是聊了個大概,各種分佈(常態、卜瓦松、二項...)自己都還有很多細節可以深挖,不過呢,先把這個基礎觀念弄懂,我覺得是最重要的。
聊聊你的看法吧!
除了天氣預報和買東西,你還在生活中看過、或感覺過哪些事情,很像可以用機率分佈來描述的?在下面留言分享看看吧!



