最近考えてたんだけど、人間って、無意識にモノをグループ分けしてるよね。本棚の本をジャンルで分けたり、音楽をアーティストで整理したり。似たものを集めて「これはこの仲間」って判断するの、たぶん生きるための基本的なスキルなんだと思う。世界を理解するための方法、みたいな。
で、20世紀半ばにコンピューターが出てきたとき、研究者たちは思ったわけだ。「これ、機械にやらせられないかな?」って。コンピューターが膨大なデータを見て、自動で「似てるやつら」を見つけ出す。そんなことができたらすごい、と。
これ、ただの学問的な好奇心じゃなかったんだよね。コンピューターが普及するにつれて、人間が手作業で整理するには多すぎるデータが生まれ始めた。だから、機械にパターンを自動で見つけてもらう必要が、マジであったわけ。
最初のヒーロー、K-meansの意外な誕生
最初の大きなブレークスルーは、実は意外な場所から来た。電話会社の研究部門、あの有名なベル研究所(Bell Labs)から。1950年代、ここのエンジニアたちは、電話の音声をどうやってもっと効率的に送るか、っていう超実用的な問題に取り組んでた。
1957年、スチュアート・ロイドっていう数学者が、アナログ信号(声とか)をデジタルデータに変換する方法を研究してた。複雑な信号を、より少ないデータ点で表現したかったんだ。そこで彼が編み出したのが、データ点を自動でグループ分けするアルゴリズム。これが後の「K-means法」の原型になったんだよね。
面白いのは、ロイド自身はこれを「クラスタリング」なんて呼んでなかったこと。彼はただ通信の問題を解きたかっただけ。彼の研究なんて、1982年まで論文化されなかったんだから。でも、この手法がデータサイエンスで最も重要なアルゴリズムの一つになるんだから、歴史って面白いよね。ちなみに、「K-means」っていう名前を付けたのは、1967年のジェームズ・マックイーンっていう社会科学者。やっと名前がついたわけだ。
で、K-meansってどうやるの?
正直、K-meansの考え方は驚くほどシンプル。
まず、最初に「グループをいくつ作りたいか(k)」を決める。これが一番のポイントであり、弱点でもあるんだけど、まあ後で話す。次に、そのk個の「中心点(セントロイド)」をデータの中に適当に置く。これが最初の仮のグループの中心。
そこからは、単純作業の繰り返し。
- 各データ点は、一番近い「中心点」のグループに所属する。
- 全データ点の所属が決まったら、各グループの「本当の中心(平均)」を計算して、そこに中心点を移動させる。
- 中心点が動いたから、また各データ点の所属が変わるかもしれない。だから、もう一回、一番近い中心点のグループに所属させる。
- これを、中心点がもうほとんど動かなくなるまで繰り返す。
これだけ。要するに、「各グループ内のデータ点と、そのグループの中心との距離の合計」を、できるだけ小さくしようとしてるだけなんだ。なるべくコンパクトなグループを作ろうぜ!って感じ。

でもね、K-meansには大きな問題があった。さっきも言ったけど、最初に「k」の数を決め打ちしなきゃいけないこと。データに自然なグループがいくつあるかなんて、普通は前もってわからないじゃん?
それに、K-meansは全てのグループがだいたい同じ大きさの「円形」だと仮定してる。でも、現実のデータはもっと複雑。細長かったり、三日月形だったりするグループには全然対応できないんだ。
「形」の壁を超えろ!階層的クラスタリングの登場
K-meansが苦手な「円じゃない形」のデータをどうにかしたい。そこで研究者たちは、まったく違うアプローチを考えた。「中心」を探すんじゃなくて、「データ点同士のつながり」に着目したんだ。
つまり、データセット内の全ての点について、総当たりで「お互いの距離」を計算する。この膨大な距離のリストを使って、一番近い点から順番につなげていく。小さな塊がだんだん合体して、大きな塊になっていくイメージ。これが「階層的クラスタリング」。
このアプローチには、大きく分けて2つの戦略があった。
- 単連結法 (Single-Linkage): すごく積極的なやつ。「クラスターAの『誰か一人』と、クラスターBの『誰か一人』が近ければ、もう合併しちゃおう!」っていう考え方。これだと、細長ーいクラスターとか、変わった形のクラスターも見つけられる。でも、たまに関係ないクラスター同士を「鎖」みたいにつなげちゃう「連鎖効果」っていう弱点があった。
- 完全連結法 (Complete-Linkage): こっちは逆にすごく慎重派。「クラスターAの『一番遠い点』と、クラスターBの『一番遠い点』ですら、まだ近いと言える場合だけ」合併する。だから、できあがるクラスターはすごくコンパクトで、球形に近くなる傾向がある。
この合併の過程を可視化したのが「デンドログラム」っていう樹形図。どの段階でどのグループがくっついたかが一目瞭然なんだ。
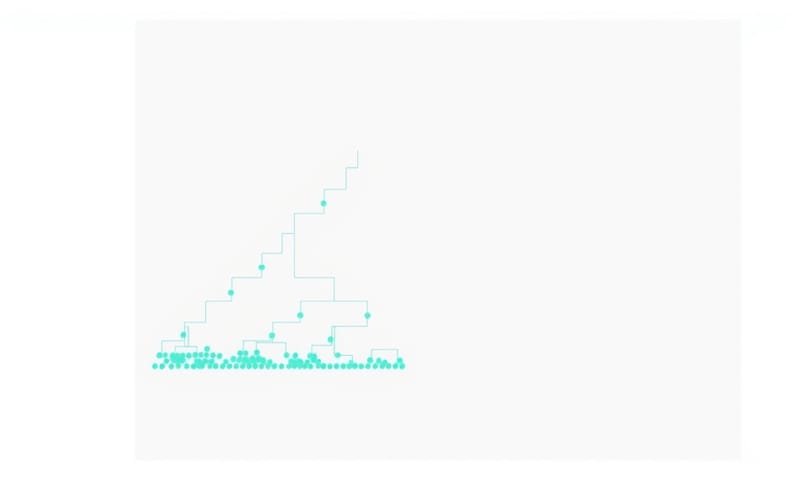
このデンドログラムのどこを水平に「切る」かで、クラスターの数を後から決められる。これはK-meansにはない大きなメリット。でも、致命的な問題があった。…とにかく遅い。データが1000個あったら、総当たりの距離計算って約50万回も必要になる。データが増えると計算量が爆発的に増えるから、大規模なデータにはまったく使えなかったんだ。
密度こそが正義!DBSCANが起こした革命
1990年代になると、もう一つの大きな問題が浮上してきた。「ノイズ」の存在だ。現実のデータには、どのグループにも属さない「はぐれ者」みたいな点がたくさん混じってる。測定エラーとか、単なる例外とか。K-meansも階層的手法も、こういうノイズを無理やりどこかのクラスターに押し込んじゃうから、結果が歪んでしまう。
「任意の形」に対応できて、「ノイズ」をちゃんと扱えて、しかも「大規模データ」にもそこそこ強い。そんな夢みたいな方法はないのか?
1996年、ミュンヘン大学の4人の研究者(Ester, Kriegel, Sander, Xu)が発表した「DBSCAN」が、まさにそれだった。
彼らのアイデアは天才的だった。「クラスターとは何か?」っていう定義そのものを変えちゃったんだ。「中心からの距離」でも「階層的なつながり」でもない。「クラスターとは、データが『密』に集まっている領域のことだ」って。そして、密な領域同士は、疎な領域によって隔てられている、と。
DBSCANは2つのシンプルなパラメータで動く。
- Epsilon (ε): ある点の「近傍」と見なす半径。
- MinPts: その半径εの中に、最低何個の点があれば「密である」と見なすか。
このルールで、全てのデータ点は「コア点(密な領域の中心部)」「ボーダー点(密な領域の端っこ)」「ノイズ点(どっちでもない、はぐれ者)」の3種類に分類される。アルゴリズムはコア点を見つけたら、そこからεの範囲内で届くコア点やボーダー点を全部つなげていく。これによって、どんなにグネグネした形でも、密度さえ続いていれば一つのクラスターとして認識できる。しかも、どこにも属せない点は「ノイズ」としてちゃんと弾かれる。これは画期的だった。

日本だと、特にWeb系のエンジニアはQiitaとかでscikit-learnを使った実装例をよく見るよね。だいたいK-meansかDBSCANから試すのが定番かな。でも、このDBSCANの原著論文なんかは、今読んでも「なるほど、こういう思想だったのか」って発見がある。アメリカの研究なんかだと、こういう理論的な背景から入ることが多い気がする。文化の違いというか、面白いよね。
で、結局どれを使えばいいの?
ここまで主要なアルゴリズムの進化を見てきたけど、「じゃあ、どれが一番いいの?」って思うよね。これ、機械学習の世界で有名な「ノーフリーランチ定理(No-Free-Lunch Theorem)」っていうのがあって、要するに「どんな問題にでも効く最強の万能アルゴリズムなんて存在しない」ってこと。
だから、データの特徴に合わせて道具を選ぶのが大事。ちょっと、それぞれのキャラをまとめてみようか。
| アルゴリズム | 得意なこと(一言で言うと) | 苦手なこと(注意点) | どんな時に使う? |
|---|---|---|---|
| K-means | とにかく速い!考え方もシンプルで、とっつきやすい。とりあえずの「初期分析」ならこいつ。 | 丸いクラスターしか見つけられない。あと、最初にクラスター数「k」を決めないといけないのが面倒。 | 顧客セグメンテーションみたいに、大まかにグループ分けしたい時。答えの速さが欲しい時。 |
| 階層的クラスタリング | クラスターがどうやって出来ていくかの過程(デンドログラム)が見えるのが面白い。解釈しやすい。 | データが増えると、もうめちゃくちゃ遅くなる。ビッグデータには絶対向かない。 | 生物の分類とか、系統樹を作りたい時みたいに、グループ間の「階層関係」が重要な場合。 |
| DBSCAN | 複雑な形もなんのその。おまけに「ノイズ」を自動で見つけてくれる優等生。クラスター数を指定しなくていいのも楽。 | 密度の違うクラスターが混在してると、パラメータ調整が地獄。一つの設定じゃ全部はうまくいかない。 | 地理データで異常な活動エリアを見つけるとか、不正検知とか、「はぐれ値」自体が意味を持つ分析。 |
| 最近の手法 (GMM, Deep Learningなど) | 「この点は80%A群、20%B群」みたいな柔軟な所属を許したり(GMM)、データの特徴自体を学習してから分類したり(深層学習)。 | 計算コストが高いし、中身がブラックボックスになりがち。なんでこの結果になったか説明しにくい。 | 画像認識とか、超高次元データとか、もはや人間の直感が通用しない複雑な問題を扱う時。 |
「良いクラスター」って、そもそも何だ?
ここまで技術の話をしてきたけど、もっと根本的な問いがある。「良いクラスターって何?」ってこと。だって、クラスタリングは教師なし学習だから、「正解」がないんだよ。アルゴリズムが出した結果が、本当に意味のあるものなのか、それともただの偶然の産物なのか、判断するのがすごく難しい。
一応、評価するための指標はいくつかある。例えば「シルエットスコア」っていうのが有名で、これは「同じクラスター内の仲間とはどれだけ近く、他のクラスターの奴らとはどれだけ遠いか」を点数化するもの。スコアが1に近いほど、良い感じに分かれてるって言える。
でも、最終的に一番大事なのは、そのクラスタリングの結果が「何かの役に立つか」どうか。ビジネス上の意思決定につながるとか、新しい科学的な発見のきっかけになるとか。結局は、ドメイン知識を持った人間が結果を解釈して、意味を見出す必要があるんだよね。
クラスタリングの歴史って、単なる技術の進化だけじゃなくて、「データから意味を見つけ出す」っていう人間の探求の歴史そのものなんだな、って思う。単純な整理整頓から始まって、今や公平性や倫理まで考えなきゃいけなくなってる。なかなか奥が深い世界だよ、本当に。
…と、ここまで色々話してきたけど、もしあなたの仕事や研究でクラスタリングを使うとしたら、どんな「グループ」を見つけてみたい?例えば、マーケティングの新しい顧客層とか、製造ラインの異常パターンとか。よかったらコメントで教えてみて。



